ball topology Say is a closed set in (in other words, open).
Say we have a sequence in and that . Then .
Proof
Let’s say .
Which is a contradiction. Because cannot converge outside QED.
complete if is complete.
Proposition
Say is a topological space, that is Hausdorff.
If is compact, then is closed.
Proof
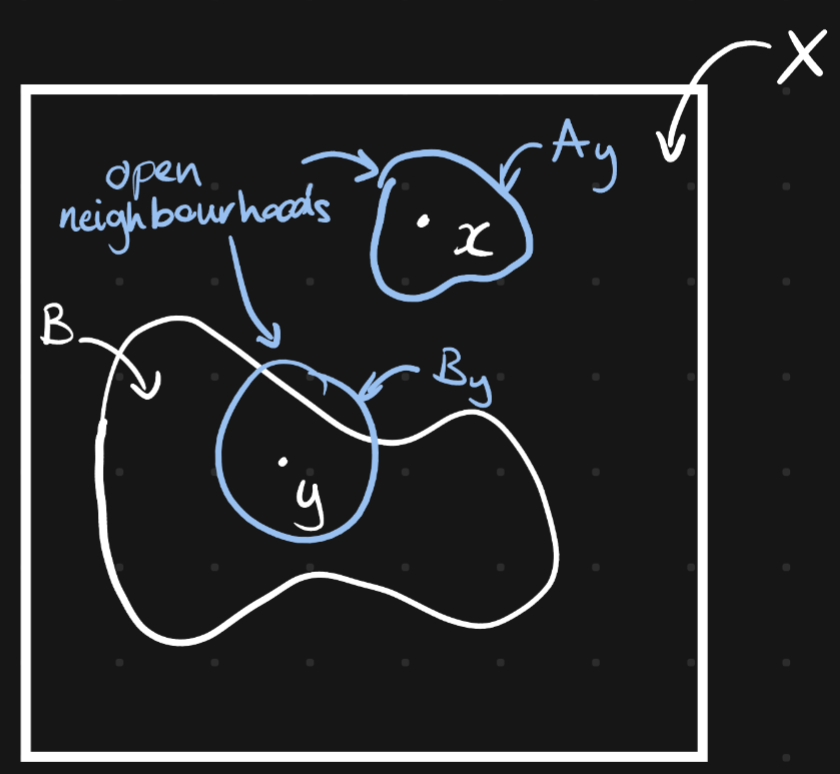 Hausdorff ⇒ , both are open.
Then is an open cover of
Hausdorff ⇒ , both are open.
Then is an open cover of
Compact ⇒ Pick out finite subcover of . Then since (for any )
So is open, in other words, is closed.
QED.
Heine-Borel Theorem
Say . Then is compact is closed and bounded.
Proof
For →: is closed since is Hausdorff and is compact, see the previous result. It is bounded since we can cover it by finitely many balls.
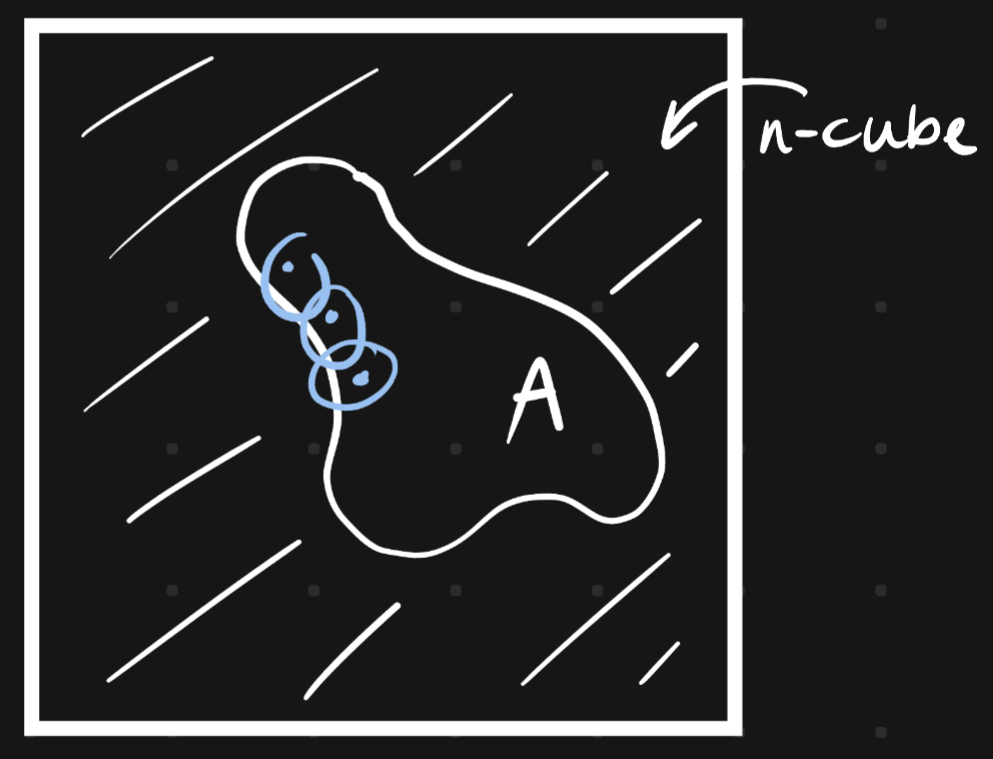
For ←: Assume first that is an -cube with boundary included.
Say is not compact. If an open cover of has no finite subcover, then by halving sides of cubes we get a sequence of cubes contained in each other, each having no finite subcover. The centres of these cubes form a Cauchy sequence with a limit .
 . Show: is complete.
Any neighbourhood of from the cover will obviously contain a small enough cube, and will be a finite subcover.
But this is a contradiction.
. Show: is complete.
Any neighbourhood of from the cover will obviously contain a small enough cube, and will be a finite subcover.
But this is a contradiction.
QED.
open. Say is an cover of . Then is an open cover of the -cube.
cover of the -cube.
Then will cover .
Cor
is locally compact Hausdorff, and -compact

Complex Vector Space Exercise
Show that finite dimensional the complex vector space for some . : Linear map:
Proof
. Say is a linear basis for . Define bijective linear map by . It is linear;
Surs. . Basis such that . So
Injective Say then , so Injective for linear map .
is a vector space is a vector space
(vectors spaces have to start from the origin, as that is where vectors themselves start from).
Metric Space Exercise
Consider the unit circle
Say there is a circle , This is a metric space for = arclength between and .
Check:
- = length of straight line between and